今回はリストについて説明します。
この連載中を通して、ずっと、numb-lambda の REPL に括弧で囲まれた式を幾つも入力してきました。多数の括弧に囲まれた「あれ」がリストなのです。なんと、LISPでは、プログラムもリストなのです。このように書くと少々、厳密さに欠きます。括弧に囲まれた「あれ」はリストの外部表現でS式と呼びます。REPL がS式をリードすると内部でリストが生成されます。何処にでしょうか。もちろん、メモリー(RAM)中にです。今回はデータとしてのリストを見てみましょう。
list 関数
ここで、list 関数を使ってみます。list 関数は、0個以上の引数を取り、それらを内包するリストを生成します。生成されるリストはデータです。
> (list 'a 'b 'c 'd 'e 'f)
(a b c d e f)
>
以上はシンボルを要素とするリストです。list は関数なので引数は全て評価された後、処理が適用されます。したがって、各シンボルはクォートしています。もし、クォートを書き忘れると、そのシンボルは評価されてしまい、バインドされている値が引数となってしまいますから注意してください。REPL は、list 式を評価すると、その結果を印字します。それが、
(a b c d e f)です。また、quote スペシャルフォームを用いて同様なリストを生成することができます。式の前に
' (アポストロフィ)を書いても quote と同じ意味になります。
> (quote (a b c d e f))
(a b c d e f)
> '(a b c d e f)
(a b c d e f)
>
list 関数を使い評価して生成したリストや、quote スペシャルフォームで生成したリストはシンボルにバインドしたり、関数の引数に渡したりしなければREPLが印字した後、任意の時期にガーベジコレクションされ失くなってしまいます。ですから、ここでは lst というシンボルにバインドしておきましょう。
> (define lst (list 'a 'b 'c 'd 'e 'f))
> lst
(a b c d e f)
> (define lst2 '(a b c d e f))
> lst2
(a b c d e f)
>
シンボル lst を評価するとバインドされたリストが得られます。印字されるものもS式になっています。これが、どのようなものかイメージするために図示してみます。

ドット対(つい)と cons、car、cdr 関数
前節のリストを構成するデータ構造をドット対(つい)または、ドッティ・ペア(dotty pair)といいます。Scheme においては、単にペア(pair)といいます。

ペアはポインタ(アドレス)を格納す領域が2つだけで構成されたデータ構造です。図では左側を car 、右側を cdr といい、それぞれ、カー、クダーと読みます。
ペアを作り出すには cons 関数を使います。ペアをひとつ、作ってみましょう。
> (cons 'x 'y)
(x . y)
>
上で見たリストとは少し違った S式が印字されました。シンボル x と y の間に . (ドット)が入っています。これを図示すると以下のようになります。
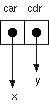
ペアの car 部は、メモリ中のどこかにある x というシンボルを指しています。同様に cdr 部は、y というシンボルを指しています。この図にあるシンボルは、あくまでモデルです。実際のシンボルは複雑なデータ構造です。
ペアの car 部と cdr 部を取り出すには、それぞれ、car、cdrという関数を使います。
> (define p (cons 'x 'y))
> p
(x . y)
> (car p)
x
> (cdr p)
y
>
空リスト
前に取り上げたリスト '(a b c d e f)をもう一度、見てみましょう。

car 部がシンボル f をポイントしているセルを見てください。
cdr 部に斜線が書いてあります。これは、空リストといって、リストの終端を表します。空リストは、'() のようなS式で表現します。他の LISP では、nil と表記するものもあります。そういった処理系において nil は論理値の偽を表すシンボルとなっています。(真を表すには、t を使います)Scheme ではリストの終端に偽の論理値(#f)を使うことは出来ません。シンボル t や nil も定義されていませんので注意が必要です。
それでは、f と等価のペアを cons してみましょう。
> (define f (cons 'f '()))
> f
(f)
> (car f)
f
> (cdr f)
'()
>
ここでは、consした後、シンボル f にバインドしています。直後に f を評価すると、(f) というS式が返ります。ここにドットはありません。cdr 部が空リストのセルは、このように表記する規則になっているだけです。
pair?という述語があります。引数がペアか、空リストなら #tを返します。
> (pair? f)
#t
> (pair? (car f))
#f
> (pair? '())
#t
> (pair? (cdr f))
#t
> (pair? (cons 'x 'y))
#t
> (pair? (cdr (cons 'x 'y)))
#f
> (pair? lst)
#t
>
list を使わず cons だけで、先程のリストを再現できます。
> (cons 'a
(cons 'b
(cons 'c
(cons 'd
(cons 'e
(cons 'f '()))))))
(a b c d e f)
>
行儀のよいリスト(proper list)では、このように最後のペアにある cdr 部が空リストになっています。反対に行儀の悪いリスト(improper list)を書いてみましょう。
> (cons 'a
(cons 'b
(cons 'c
(cons 'd
(cons 'e
(cons 'f 'g))))))
(a b c d e f . g)
>
このように、S式には . ドットが表われました。これも、S式の表記規則だと理解してください。図にすると以下のようになります。

proper list '(a b c d e f)に戻りましょう。
これから最初の要素を取り出します。
> (car '(a b c d e f))
a
>
このリストのcdrを取ると、どうなるでしょうか。
> (cdr '(a b c d e f))
(b c d e f)
>
では、e を取り出すには、どうすれば良いでしょうか。
> (cdr '(a b c d e f))
(b c d e f)
> (car
(cdr
(cdr
(cdr
(cdr '(a b c d e f))))))
e
>
空リストかどうか判定する述語があります。null? です。
> (null? '())
#t
> (null? '(a b c d e f))
#f
> (null?
(cdr
(cdr
(cdr
(cdr
(cdr
(cdr '(a b c d e f))))))))
#t
>
リストの長さを計測してみましょう。
> (let len ((ls '(a b c d e f)) (i 0))
(if (null? ls)
i
(len (cdr ls) (+ i 1))))
6
>
実は、length という関数があります。
> length
<procedure>
> (length '(a b c d e f))
6
>
リストを逆順に並べ換えてみましょう。
> (let rev ((ls '(a b c d e f))(acc '()))
(if (null? ls)
acc
(rev (cdr ls) (cons (car ls) acc))))
(f e d c b a)
>
これも、reverseという関数が用意されています。
> reverse
<procedure>
> (reverse '(a b c d e f))
(f e d c b a)
>
それでは、最後にフィボナッチ数列を生成する関数を書きます。
> (define fib
(lambda ()
(let f ((a 1)(b 1)(acc '()))
(if (<= a 0)
(reverse acc)
(f b (+ a b) (cons a acc))))))
> (fib)
(1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817 39088169 63245986 102334155 165580141 267914296 433494437 701408733 1134903170 1836311903)
> (length (fib))
46
> (reverse (fib))
(1836311903 1134903170 701408733 433494437 267914296 165580141 102334155 63245986 39088169 24157817 14930352 9227465 5702887 3524578 2178309 1346269 832040 514229 317811 196418 121393 75025 46368 28657 17711 10946 6765 4181 2584 1597 987 610 377 233 144 89 55 34 21 13 8 5 3 2 1 1)
> (length (reverse (fib)))
46
>
今回の fib は、副作用を使っていません。これが関数型プログラミングの例です。他のリストを扱う関数と結合して、さまざまなことが出来ることが解ると思います。
力試しに、行儀の良いリストの n 番目の要素を返す関数を書いてみてください。
次回は、何を取り上げるか検討中です。そろそろ、プログラムを書いていくのもいいですね。